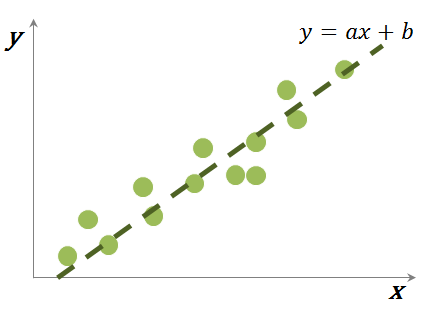Linear Regression Operator

---

Operator 설명

• 종속 변수 Y와 하나 이상의 독립 변수 X와의 선형 상관 관계를 모델링하는 방법이다.
• 선형 회귀는 주어진 데이터를 대표하는 하나의 직선을 찾는 것인데 이 선을 함수로 표현하면 y=ax+b가 된다. a를 가중치(weight)라고 말한다. 알고리즘은 Spark ml의 LinearRegression 알고리즘을 사용하여 구현하였다.

Operator 파라미터 설명

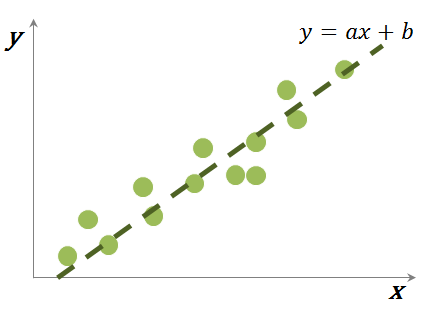
• labelName: 라벨 이름 (required)
• regParam: Regularization parameter 설정 (>= 0) (required)
• elasticNetParam: ElasticNet 설정 (required)
  • alpha = 0, L2 penalty (ridge penalty와 같다.)
  • alpha = 1, L1 penalty (Lasso penalty와 같다.)
  • alpha =0과1사이, L1 과 L2의 combination.(elastic net)
• maxIter: LinearRegression을 한번 수행할 때 수행되는 최대 반복 횟수. 최대 시도 횟수 (required)
• tolerance: convergence tolerance 설정 (required)

작동 순서

1. 입력 DataFrame의 유효성 검사를 진행한다. (Label column, Numeric Columns)
2. 입력 DataFrame 중 라벨 칼럼을 제외한 나머지 모든 칼럼을 Vectors로 변환하여 features 칼럼으로 만든다.
3. Spark ml의 LinearRegression 알고리즘을 사용한다. (가중치를 구한다.)
4. 출력 DataFrame을 생성한다.

Operator 모듈 테스트 결과

입력 데이터

label	a1	a2	a3	a4	a5
88.01632464	0.636574028	8.442168148	2.116099574	2.771867529	8.448426549
138.7548543	4.595454155	4.388041662	4.926093835	2.682403955	8.617751819
38.28387155	4.292060076	0.861090232	9.15798394	6.607498138	4.084605081
82.14778398	8.559949469	3.856237673	1.0381353	1.687798024	2.8930632
33.79002054	2.272320698	1.834078721	6.300620501	1.93796937	2.069888374
7.38866956	3.956280442	0.34429275	4.337370526	7.563450458	8.591228627
191.4532705	2.220060635	7.843024669	6.462687043	8.731893832	9.28188111
15.34906002	6.105141656	1.074919676	1.162823303	9.241172289	7.23885872
97.40527838	2.691071171	3.571957641	7.805965771	6.843146634	3.053870888
111.4973958	4.262579387	7.369277727	0.820670523	6.687792013	3.976156809

결과 데이터

index	attribute	weight
1	a1	14.876713421499904
2	a2	22.527385416531974
3	a3	13.075232570485753
4	a4	0.06384440492653287
5	a5	4.089080128867606

• LinearRegression은 supervised learning이므로 label이 학습 data로 사용된다. label은 y=wx+b에서 y값으로 사용된다.
• 주어진 data들로 학습한 후 각 column(a1~a5)에 대한 weight 값을 얻을 수 있고 원하는 선형모델을 얻을 수 있다.
• parameter 설정은 다음과 같다.

val linearRegressionInfo =
  LinearRegressionInfo.newBuilder()
    .setLabelName("label")
    .setRegParam(0.0)
    .setElasticNetParam(0.0)
    .setMaxIter(100)
    .setTolerance(0.05)
    .build